Instability and Chaos in Fault Sliding due to Asymmetric Friction and Negative Stiffness
Instability of sliding resisted by friction and the following chaotic motion of the sliding surfaces is observed across the scales from cutting tools to faults in the Earth’s crust. Understanding instability and chaos associated with sliding over faults is especially important, as this sliding is one of the mechanisms of earthquakes. At a lower scale fault sliding is a mechanism of rockbursts – dangerous rock fall in underground mining excavations that is capable of causing fatalities and financial loss. A new form of asymmetric friction was discovered by (Bafekrpour et al., 2015). Anisotropic (e.g. layered) materials or rocks with the anisotropy axes inclined to the contact surface and being placed in constrained environment show the effect of asymmetric friction whereby resistance to sliding in one direction is considerably (several times) smaller than resistance to sliding in the opposite direction [13]. Subsequently the fault would exhibit different behaviour (e.g. from sliding to non-sliding) depending upon the direction of shear loading. Furthermore, areas with asymmetric friction can produce partial sliding over the fault and trigger the total instability (major sliding). Especially interesting is the performance of asymmetric friction patches under vibrations caused for instance by sliding of nearby faults and a possibility of triggering major sliding. Given that anisotropic, in particular foliated rock, is a common occurrence in nature the above effects of asymmetric friction can play a considerable role in generation of earthquakes or rockbursts. Modelling highly non-linear behaviour typical for friction required considerable computational resources, which necessitates the use of HPC.
Area of science
Solid Mechanics
Systems used
Magnus
Applications used
Python and MatlabThe Challenge
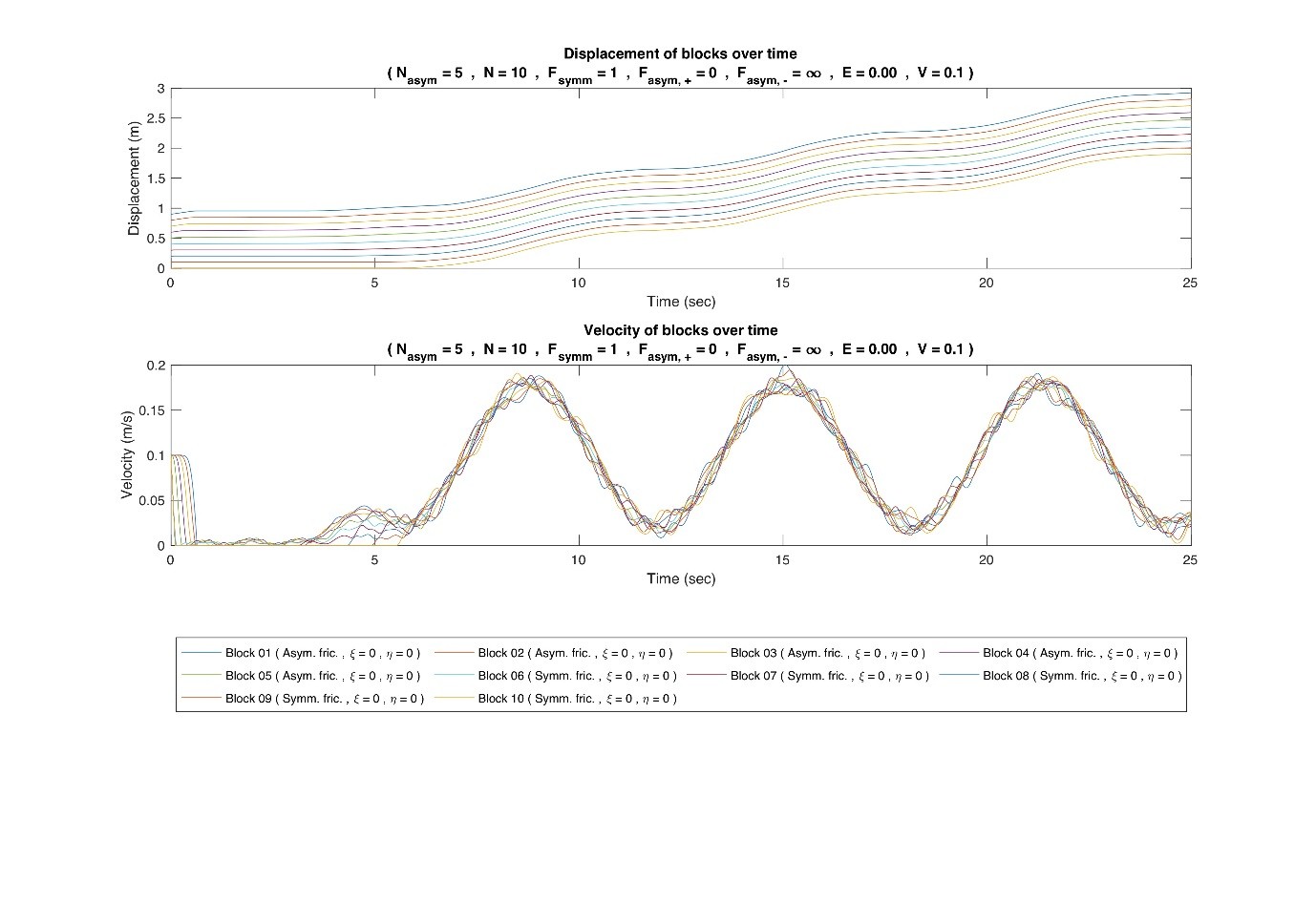
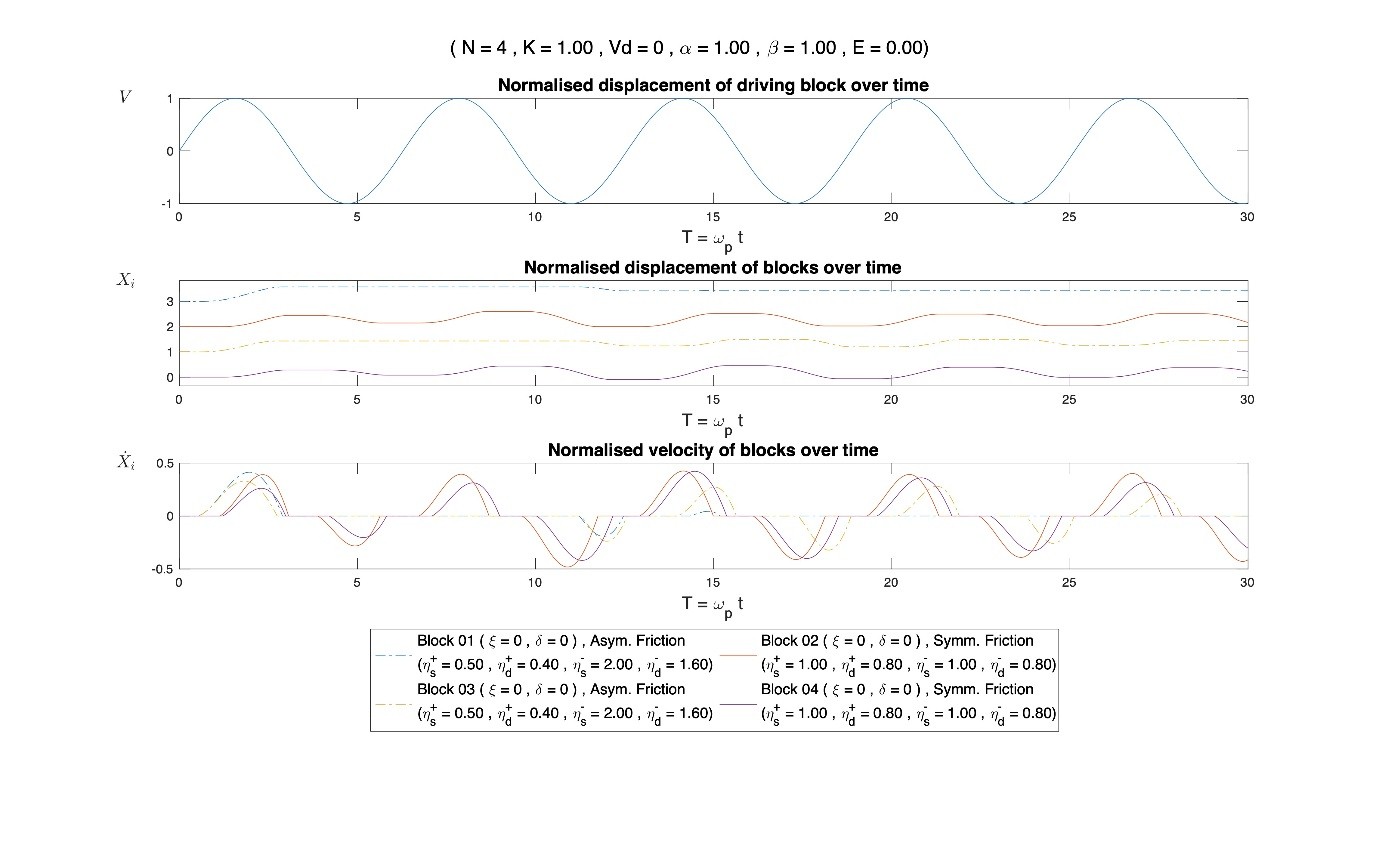
The aims of the project are: (1) determining the conditions of instability, chaos and the associated seismicity in Burridge-Knopoff blocky model of fault sliding with different percentages of blocks having asymmetric friction and different percentages of connecting springs having negative stiffness; (2) determining the conditions of emergence of solitary waves in systems with negative stiffness elements; (3) identifying the conditions of symmetry breaking in systems of blocks with conventional friction law under symmetrical external loading.
The Solution
The problem in question was reduced to a set of stiff ordinary differential equations modelling the movement of clocks with symmetric and asymmetric friction connected by positive and negative stiffness springs. The system of equations is solved numerically, and parametric analysis is used to investigate the effects of varying parameters.
The Outcome
With the help of Magnus Supercomputing, large combinations of parameters were investigated in the parametric analysis in a timely manner, Wong et al (2018). Performing the search of instability due to asymmetric friction as well as the scalability we also provided a basis for a method of utilizing the vibration in energy harvesting.
List of Publications
Wong, R, Pasternak, E & Dyskin, A 2019a, ‘Asymmetric friction effects in interblock interaction’, Smart Construction Workshop, Perth, WA, Australia, 27 – 28 November 2019.
Wong, R, Pasternak, E & Dyskin, A 2020a, ‘Asymmetric friction effects on surface interaction’. General Assembly of European Geosciences Union, Vienna, Austria, 4-8 May 2020, EGU2020-22426, https://doi.org/10.5194/egusphere-egu2020-22426, 2020. Presented in EGU 2020 online presentation.
Wong, R, Pasternak, E & Dyskin, A 2020b, ‘Sliding oscillations of a fault in the presence of asymmetric friction’ – in preparation for Int. J Eng. Sci.

Figure 1. Alternating asymmetric and symmetric friction block in a vibrating environment, showing how steadily reoccurring instability can be achieve with the presence of asymmetric friction, with a selected combination of parameters, Wong et al. (2020a,b)